
| ( 579 ) | Numb. 196. | |
|
T R A N S A C T I O N S.* 1. THE Preface. 2. A Paper of the Honourable Robert Boyle,* late Fellow of the Royal Society,* deposited with Secretaries of the R. S. A°. 1680. containing a Method of Preparing the Phosphorus of Humane Urine. 3. A Solution of the Florentine Problem touching the Figure of a Cupola, whose Windows being cut out, the Remainder is Quadrable. By the Reverend John Wallis,* S.T.D. 4. The Extract of two Letters from Mr. Anth. Leeuwenhoek* of Delft about the Testicles of a Rat, and the Ammalcules therin contained; with some Observations of Small Animals found in Oysters, and the Sap of Vines. 5. Some Observatios in the dissection of a Rat, with a Figure of the Genital parts thereof. By Mr. Ric. Waller, S. R. Secr. 5.[!] An Estimate of the Degrees of the Mortality of Mankind, drawn from curious Tables of the Births and Funerals at the City of Breslaw,* with an Attempt to ascertain the|<580> Price of Annuities* upon Lives. By Mr. Edmond Halley, R. S. S. An Account of B O O K S. 1. THE WISDOM OF GOD manifested in the Works of the Creation: In two Parts. The Second Edition, very much enlarged. By John Ray,* S. R. S. in 8°. 1692. 2. Three Physico-Theological Discourses, concerning 1. The Primitive Chaos and Creation of the World 2. The General Deluge, its Causes and Effects. 3. The Dissolution of the World, and future Conflagration, in 8°. 1693. Both Printed for S. Smith. 3. Leonardi Plukenetii Phytographia, sive stirpium illustrorum Icones. Pars Tertia. Lond. In Folio. 1693. Printed for the Author, and Sold by S. Smith.
|
||
THE Contemplation of the Mortality of Mankind, has besides the Moral, its Pysical and Political Uses, both which have been some years since most judicously considered by the courious Sir Willian Petty,* in his Natural and Political Observations on the Bills of Mortality of London,* owned by Captain John Graunt.* And since in al like a Treatise on the Bills of Morality of|<597> Dublin. But the Deduction from those Bills of Mortality seemed even to their Authors to be defective: First, In that the Number of the People was wanting. Secondly, That the Ages of the People dying was not to be had. And Lastly, That both London and Dublin* by reason of the great an casual Accession of Strangers who die therein, (as appeared in both, by the great Excess of the Funerals above the Births) rendered them incapable of being Standards for this purpose; which requieres, if it were possible, that the People we treat of should not at alle be changed, but die where they were born, without any Adventitious Increase from Abroad, or Decay by Migration elsewhere.
This Defect seems in a great measure to be satisfied by the late curious Tables of the Bills of Mortality at the City of Breslaw, lately communicated to this Honourable Society by Mr. Justell, wherein both the Ages and Sexes of all that die are monthly delivered, and compared wiht the number of the Births, for Five Years last past, viz. 1687, 88, 89, 90, 91, seeming to be done with all the Exactness and Sincerity possible.
This City of Breslaw is the Capital City of the Province of Silesia; or, as the Germans call it, Schlesia, and is situated on the Western Bank of the River Oder, anciently called Viadrus; near the Confines of Germany and Poland, and very near the Latitude of London. It is very far from the Sea, and as much a Mediterranean Place as can be desired, whence the confluence of Strangers is but small, and the Manufacture of Linnen employs chiefly the poor People of the place, as well as of the Country round about; whence comes that sort of Linnen we usually call your Sclesie Linnen; which is the chief, if not the only Merchandize of the place. For these Reasons the People of this City seem most pro-|<598>per for a Standard; and the rather, for that the Births do, a smaller matter, exceed the Funerals. The only thing wanting is the Number of the whole People, which in some measure I have endeavoured to supply by comparison of the Mortality of the People of all Ages, which I shall from the said Bill trace out with all the Accuracy possible.
It appears that in the Five Years mentioned, viz. from 87 to 91 inclusive, there were born 6193 Persons, and buried 5869; that is, born per Annum 1238, and buried 1174; whence an Encrease of the People may be argued of 64 per Annum, of of about a 20th part, which may perhaps be ballanced by the Levies for the Emperor’s Service in his Wars. But this being contingent, and the Births certain, I will suppose the People of Breslaw to be encreased by 1238 Births annually. Of these it appears by the same Tables, that 348 do die yearly in the first Year of their Age, and that but 890 do arrive at a full Years Age; and likewise, that 198 do die in the Five Years between 1 and 6 compleat, taken at a Medium; so that but 692 of the Persons born do survive Six whole Years. From this Age the Infants being arrived at some degree of Firmness, grow less and less Mortal; and it appears that of the whole People of Breslaw there die yearly, as in the following Table, wherein the upper Line shows the Age, and the next under it the Number of Persons of that Age dying yearly.|<599>
| 7 | 8 | 9 | . | 14 | . | 18 | . | 21 | . | 27 | 28 | . | 35 |
| 11 | 11 | 6 | 5½ | 2 | 3½ | 5 | 6 | 4½ | 6½ | 9 | 8 | 7 | 7 |
| 36 | . | 42 | . | 45 | . | 49 | 54 | 55 | 56 | . | 63 | . | 70 |
| 8 | 9½ | 8 | 9 | 7 | 7 | 10 | 11 | 9 | 9 | 10 | 12 | 9½ | 14 |
| 71 | 72 | . | 77 | . | 81 | . | 84 | . | 90 | 91 | 98 | 99 | 100 |
| 9 | 11 | 9½ | 6 | 7 | 3 | 4 | 2 | 1 | 1 | 1 | 0 | 1/5 | 3/5 |
And where no Figure is placed over, it is to be understood of those that die between the Ages of the preceding and consequent Column.
From this Table it is evident, that from the Age of 9 to about 25 there does not die above 6 per Annum of each Age, which is much about one per Cent. of those that are of those Ages: And wheras in the 14, 15, 16, 17 Years there appear to die much fewer, as 2 and 3½, yet that seems rather to be attributed to Chance, as are the other Irregularities in the Series of Ages, which would rectifie theselves, were the nuber of Years much more considerable, as 20 instead of 5. And by our own Experience in Christ-Church Hospital, I am informed there die of the Young Lads, much about one per Cent. per Annum, they being of the foresaid Ages. From 25 to 50 there seem to die from 7 to 8 and 9 per Annum of each Age; and after that to 70, they growing more crasie, though the number be much diminished, yet the Mortality encreases, and there are found to die 10 or 11 of each Age per Annum: From thence the number of the Living being grown very small, they|<600> gradually decline till there be none left do die; as my be seen at one View in the Table.
From these Considerations I have formed the adjoyned Table, whose Uses are manifold, and give a more just Idea of the State and Condition of Mankind, than any thing yet extant that I know of. It exhibits the Number of People in the City of Breslaw of all Ages, from the Birth to extream Old Age, and thereby shews the Chances of Mortality at all Ages, and likewise how to make a certain Estimate of the value of Annuities for Lives, which hitherto has been only done by an imaginary Valuation: Also the Chances that there are that a Person of any Age proposed does live to any other Age given; with many more, as I shall hereafter shew. This Table does shew the number of Persons that are living in the Age current annexed thereto, as follows:
|
|
Thus it appears, that the whole People of Breslaw does consist of 34000 Souls, being the Sum Total of the Persons of all Ages in the Table: The first use hereof|<601> is to shew the Proportion of Men able to bear Arms in any Multitude, which are those between 18 and 56, rather than 16 and 60; the one being generally too weak to bear the Fatigues of War and the Weight of Arms, and the other too crasie and infirm from Age, nonwithstanding particular Instances to the contrary. Under 18 from the Table, are found in this City 11997 Persons, and 3950 above 56, which together make 15947. So that the Residue to 34000 being 18053 are Persons between those Ages. At least one half thereof are Males, or 9027: So that the whole Force this City can raise of Fencible Men, as the Scotch call them, is about 9000 or 9/34, or somewhat more than a quarter of the Number of Souls, which may perhaps pass for a Rule for all other places.*
The Second Use of this Table is to shew the differing degrees of Mortality, or rather Vitality in all Ages; for if the number of Persons of any Age remaining after one year, be divided by the difference between that and the number of the Age proposed, it shews the odds that there is, that a Person of that Age does not die in a Year. As for Instance, a Person of 25 Years of Age has the odds of 560 to 7 or 80 to 1, that he does not die in a Year: Because that of 567, living of 25 years of Age, there do die no more than 7 in a Year, leaving 560 of 26 Years old.*
So likewise for the odds, that any Person does not die before he attain any proposed Age: Take the number of the remaining Persons of the Age proposed, and divide it by the difference between it and the number of those of the Age of the Party proposed; and that shews the odds there is between the Chances of the Party’s living or dying. As for Instance; What is the odds that a Man of 40 lives 7 Years: Take the number of Persons of 47 years, which in the Table is 377, and|<602> subtract it from the number of Persons of 40 years, which is 445, and the difference is 68: Which shews that the Persons dying in that 7 years are 68, and that it is 377 to 68 or 5½ to 1, that a Man of 40 does live 7 Years. And the like for any other number of Years.
Use III. But if it be enquired at what number of Years, it is an even Lay that a Person of any Age shall die, this Table readily performs it: For if the number of Persons living of the Age proposed be halved, it will be found by the Table at what Year the said number is reduced to half by Mortality; and that is the Age, to which it is an even Wager, that a Person of the Age proposed shall arrive before he die. As for Instance; A Person of 30 Years of Age is proposed, the number of that Age is 531, the half thereof is 265, which number I find to be between 57 and 58 Years; so that a Man of 30 may reasonably expect to live between 27 and 28 Years.*
Use IV. By what has been said, the Price of Insurance upon Lives ought to be regulated, and the difference is discovered between the price of ensuring the Live of a Man of 20 and 50, for Example: it being 100 to 1 that a Man of 20 dies not in a year, and but 38 to 1 for a Man of 50 Years of Age.
Use V. On this depends the Valuation of Annuities upon Lives; for it is plain that the Purchaser ought to pay for only such a part of the value of the Annuity, as he has Chances that he is living; and this ought to be computed yearly, and the Sum of all those yearly Values being added together, will amount to the value of the Annuity for the Life of the Person proposed. Now the present value of Money payable after a term of years, at any given rate of Interest, either may be had from Tables already computed; or almost as compendiously,|<603> by the Table of Logarithms: For the Arithmetical Complement of the Logarithm of Unity and its yearly Interest (that is, of 1, 06 for Six per Cent. being 9, 974694.) being mulitplied by the number of years proposed, gives the present value of One Pound payable after the end of so many years. Then by the foregoing Proposition, it will be as the number of Persons living after that term of years, to the number dead; so are the Odds that any one Person is Alive or Dead. And by consequence, as the Sum of both or the number of Persons living of the Age first proposed, to the number remaining after so many years, (both given by the Table) so the present value of the yearly Sum payable after the term proposed, to the Sum which ought to be paid for the Chance the person has to enjoy such an Annuity after so many Years. And this being repeated for every year of the persons Life, the Sum of all the present Values of those Chances is the true Value of the Annuity. This will without doubt appear to be a most laborious Calculation, but it being one of the principal Uses of this Speculation, and having found some Compendia for the Work, I took the pains to compute the following Table, being the short Result of a not ordinary number of Arithmetical Operations; It shews the Value of Annuities for every Fifth Year of Age, to the Seventieth, as follows.
| Age. | Years Purchase. | Age. | Years Purchase. | Age. | Years Purchase. |
|---|---|---|---|---|---|
| 1 | 10,28 | 25 | 12,27 | 50 | 9,21 |
| 5 | 13,40 | 30 | 11,72 | 55 | 8,51 |
| 10 | 13,44 | 35 | 11,12 | 60 | 7,60 |
| 15 | 13,33 | 40 | 10,57 | 56 | 6,54 |
| 20 | 12,78 | 45 | 9,91 | 70 | 5,32 |
|<604>
This shews the great Advantage of putting Money into the present Fund lately granted to their Majesties, giving 14 per Cent. per Annum, or at the rate of 7 years purchase for a Life; when young Lives, at the usual rate of Interest, are worth above 13 years Purchase. It shews likewise the Advantage of young Lives over those in Years; a Life of Ten Years being almost worth 13½ years purchase, whereas one of 36 is worth but 11.
Use V[I]. Two Lives are likewise valuable by the same Rule; for the number of Chances of each single Life, found in the Table, being mulitplied together, become the Chances of the Two Lives. And after any certain Term of Years, the Product of the two remaining Sums is the Chances that both the Persons are living. The Product of the two Differences, being the numbers of the Dead of both Ages, are the Chances that both the Persons are dead. And the two Products of the remaining Sums of the on Age multiplied by those dead of the other, shew that Chances that there are that each Party survieves the other: Whence is derived the Rule to estimate the value of the Remainder of one Life after another. Now as the Product of the Two Numbers in the Table for the Two Ages proposed, is to the difference between that Product and the Product of the two numbers of Persons deceased in any space of time, so is the value of a Sum of Money to be paid after so much time, to the value thereof und the Contingency of Mortality. And as the aforesaid Product of the two Numbers answering to the Ages proposed, to the Product of the Deceased of one Age mulitplied by those remaining alive of the other; So the Value of a Sum of Money to be paid after any time proposed, to the value of the Chances that the one Party has that he survives the other whole number of Deceased you made use of, in the second Term of the proportion. This perhaps|<605> may be better understood, by putting N for the number of the younger Age, and n for that of the Elder; Y, y the deceased of both Ages respectively, and R, r for the Remainders; and R + Y = N and r + y = n. Then shall N n be the whole number of Chances; N n - Y y be the Chances that one of the two Persons is living, Y y the Chances that they are both dead; R y the Chances that the elder Person is dead and the younger living; and r Y the Chances that the elder is living and the younger dead. Thus two Person of 18 and 35 are proposed, and after 8 years these Chances are required. The Numbers for 18 and 35 are 610 and 490, and there are 50 of the First Age dead in 8 years, and 73 of the Elder Age. There are in all 610 × 490 or 298900 Chances; of these there are 50 × 73 or 3650 that they are both dead. And as 298900, to 298900 - 3650, or 295250: So is the present value of a Sum of Money to be paid after 8 years, to the present value of a Sum to be paid if either of the two live. And as 560 × 73, so are the Chances that the Elder is dead, leaving the Younger; and as 417 × 50, so are the Chances that the Younger is dead, leaving the Elder. Wherefore as 610 × 490 to 560 × 73, so is the present value of a Sum to be paid at eight years end, to the Sum to be paid for the Chance of the Youngers Survivance; and as 610 × 490 to 417 × 50, so is the same present value to the Sum to be paid for the Chance of the Elders Survivance.
This possibly may be yet better explained by expounding these Products by Rectangular Parallelograms, as in Fig. 7 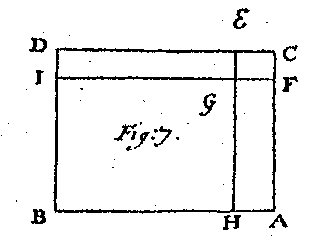 wherein A B or C D represents the number of persons of the younger Age, and D E, B H those remaining alive after a certain term of years; whence C E will answer the number of those dead in that time; So A C, B D may represent the number|<606> of the Elder Age; A F,B I the Survivors after the same term; and C F, D I, those of that Age that are dead at that time. Then shall the whole Prallelogram A B C D be N n, or the Product of the two Numbers of persons, representing such a number of Persons of the two Ages given; and by what was said before, after the Term proposed the Rectangle H D shall be as the number of Persons of the younger Age that survive, and the Rectangle A E as the number of those that die. So likewise the Rectangles A I, F D shall be as the Numbers, living and dead, of the other Age. Hence the Rectangle H I shall be as an equal number of both Ages surviving. The Rectangle F E being the Product of the decease, or Y y, an equal number of both dead. The Rectangle G D or R y, a number living of the younger Age, an dead of the Elder: And the Rectangle A G or R Y a number living of the Elder Age, but dead of the younger. This being understood, it is obvious, that as the whole Rectangle A D or N n is to the Gnomon F A B D E G or N n - Y y, so is the whole number of Persons or Chances, to the number of Chances that one of the two Persons is living, And as A D or N n is to F E or Y y, so are all the Chances, to the Chances that both are dead; whereby may be computed the value of the Reversion after both Lives. And as A D ot G D or R y, so the whole number of Chances, to the Chances that the younger is living and the other dead; wherby may be cast up what value ought to be paid for the Reversion of one Life after another, as in the case of providing for Clergy-mens Widows and others by such Reversions. And as A D to A G or r Y, so are all the Chances, to those that the Elder survires the younger. I have been the more particular, and perhaps tedious, in this matter, because it is the Key to the Case of Three Lives, which of it self would not have been so easie to comprehend.
wherein A B or C D represents the number of persons of the younger Age, and D E, B H those remaining alive after a certain term of years; whence C E will answer the number of those dead in that time; So A C, B D may represent the number|<606> of the Elder Age; A F,B I the Survivors after the same term; and C F, D I, those of that Age that are dead at that time. Then shall the whole Prallelogram A B C D be N n, or the Product of the two Numbers of persons, representing such a number of Persons of the two Ages given; and by what was said before, after the Term proposed the Rectangle H D shall be as the number of Persons of the younger Age that survive, and the Rectangle A E as the number of those that die. So likewise the Rectangles A I, F D shall be as the Numbers, living and dead, of the other Age. Hence the Rectangle H I shall be as an equal number of both Ages surviving. The Rectangle F E being the Product of the decease, or Y y, an equal number of both dead. The Rectangle G D or R y, a number living of the younger Age, an dead of the Elder: And the Rectangle A G or R Y a number living of the Elder Age, but dead of the younger. This being understood, it is obvious, that as the whole Rectangle A D or N n is to the Gnomon F A B D E G or N n - Y y, so is the whole number of Persons or Chances, to the number of Chances that one of the two Persons is living, And as A D or N n is to F E or Y y, so are all the Chances, to the Chances that both are dead; whereby may be computed the value of the Reversion after both Lives. And as A D ot G D or R y, so the whole number of Chances, to the Chances that the younger is living and the other dead; wherby may be cast up what value ought to be paid for the Reversion of one Life after another, as in the case of providing for Clergy-mens Widows and others by such Reversions. And as A D to A G or r Y, so are all the Chances, to those that the Elder survires the younger. I have been the more particular, and perhaps tedious, in this matter, because it is the Key to the Case of Three Lives, which of it self would not have been so easie to comprehend.
VII. If Three Lives are proposed, to find the value of an Annuity during the continuance of any of those three Lives. The Rule is, As the Product of the continual mulitplication of the Three Numbers, in the Table, answering to the Ages proposed, is to the difference of that Product and of the Product of the Three Numbers of the deceased of those Ages, in any given term of Years; So is the present value of a Sum of Money to be paid certainly after so many Years, to the present value of the same|<607> Sum to be paid, provided one of those three Persons be living at the Expiration of that term. Which proportion being yearly repeated, the Sum of all those present values will be the value of an Annuity granted for three such Lives. But to explain this, together with all The Cases of Survivance in three Lives: Let N be the Number in the Table for the Younger Age, n for the Second, and v for the Elder Age; let Y be those dead of the Younger Age in the term proposed, y those dead of the Second Age, and υ those of the Elder Age; and let R be the Remainder of the younger Age, r that of the middle Age and e the Remainder of the Elder Age. Then shall R + Y be equal to N; r + y to n, and ρ + υ to v, and the continual Product of the three Numbers N n v shall be equal to the continual Product of R A × r + Y × ρ + υ, which being the whole number of Chances for three Lives is computed of the eight Products following. (1) R r ρ, which is the number of Chances that all three of the Person are living. (2) r ρ Y, which ist the number of Chances that the two Elder Persons are living, and the younger dead. (3) R ρ y the number of Chances that the middle Age is dead, and the younger and Elder living. (4)R r v being the Chances that the two younger are living, and the elder dead. (5) ρ Y y the Chances that the two younger are dead, and the elder living (6) r Y υ the chances that the younger and elder are dead, and the middle Age living. (7) R y υ, which are the Chances that the younger is living and the two other dead. And Lastly and Eightly, Y y υ, which are the Chances that all three are dead. Which latter subtracted from the whole number of Chances N n v, leaves N n v - Y y υ the Sum of all other Seven Products; in ll of which one or more of the three Persons are surviving.
To make this yet more evident, I have added Fig. 8 wherein these Eight several Products are at one view exhibited. Let the rectangled Parallelepipedon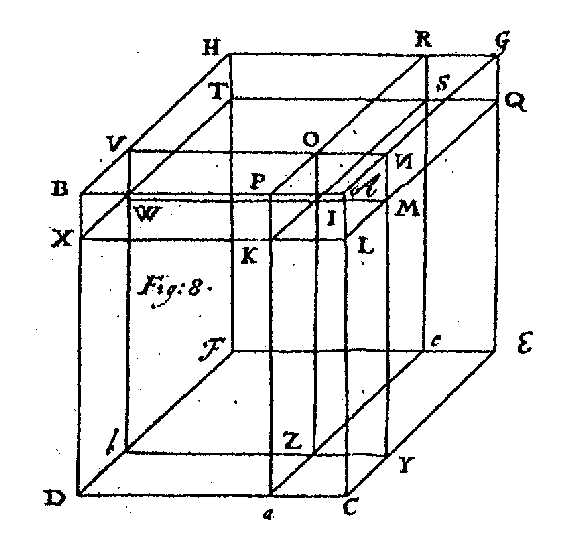 A B C D E F G H be constituted of the sides A B, G H &c. proportional to N the number of the younger Age; A C, B D &c. proportional to n e or v. And the whole Parallelepipedon shall be as the Product N y n, or our whole number of Chances. Let B P be as R, and A P as Y; let C L be as r, and L n as y; and G N as ρ, and N A as υ; and let the Plain P R e a be made parallel to the|<608> plain A C G E; the plain N V b Y parallel to A B C D; and the plain L × T Q parallel to the plain A B G H. And our first Product R r ρ shall be as the Solid S T W I F Z e b. The Second, or r ρ Y will be as the Solid E Y Z e Q S M I. the Third R ρ y, as the Solid R H O V W I S T. And the Fourth, R r v, as the Solid Z a b D W X I K. Fifthly, ρ Y y, as the Solid G Q R S I M N O. Sixthly, r Y v, as I K L M G Y Z A. Seventhly R Y υ, as the Solid I K P O B X V W. And Lastly, A I K L M N O P will be as the Product of the 3 numbers of persons dead, or Y y v. I shall not apply this in all the cases therof for brevity sake; only to shew in one how all the rest may be performed, let it be demanded what is the value of the Reversion of the younger Live after the two elder proposed. The proportion is as the whole number of Chances, N m b to the Product R y v, so is the certain present value of the Sum payable after any term propsed, to the value due to such Chances as the younger person has to bury both the elder, by the term proposed; which therfor he is to pay for. Here it is to be noted, that the first term of all these Proprotions is the same throughout, viz. N n v. The Second changing yearly according to the Decrease of R, r, ρ, and Encrease of Y, y, υ. And the thier are successively the present values of Money payable after one, two, three &c. years, according to the rate of Interest agreed on. These numbers, which are in all cases of Annuities of necessary use, I have put into the following Table, they being the Decimal values of One Pund payable after the number of years in the Margent, at the rate of 6 per Cent.|<609>
A B C D E F G H be constituted of the sides A B, G H &c. proportional to N the number of the younger Age; A C, B D &c. proportional to n e or v. And the whole Parallelepipedon shall be as the Product N y n, or our whole number of Chances. Let B P be as R, and A P as Y; let C L be as r, and L n as y; and G N as ρ, and N A as υ; and let the Plain P R e a be made parallel to the|<608> plain A C G E; the plain N V b Y parallel to A B C D; and the plain L × T Q parallel to the plain A B G H. And our first Product R r ρ shall be as the Solid S T W I F Z e b. The Second, or r ρ Y will be as the Solid E Y Z e Q S M I. the Third R ρ y, as the Solid R H O V W I S T. And the Fourth, R r v, as the Solid Z a b D W X I K. Fifthly, ρ Y y, as the Solid G Q R S I M N O. Sixthly, r Y v, as I K L M G Y Z A. Seventhly R Y υ, as the Solid I K P O B X V W. And Lastly, A I K L M N O P will be as the Product of the 3 numbers of persons dead, or Y y v. I shall not apply this in all the cases therof for brevity sake; only to shew in one how all the rest may be performed, let it be demanded what is the value of the Reversion of the younger Live after the two elder proposed. The proportion is as the whole number of Chances, N m b to the Product R y v, so is the certain present value of the Sum payable after any term propsed, to the value due to such Chances as the younger person has to bury both the elder, by the term proposed; which therfor he is to pay for. Here it is to be noted, that the first term of all these Proprotions is the same throughout, viz. N n v. The Second changing yearly according to the Decrease of R, r, ρ, and Encrease of Y, y, υ. And the thier are successively the present values of Money payable after one, two, three &c. years, according to the rate of Interest agreed on. These numbers, which are in all cases of Annuities of necessary use, I have put into the following Table, they being the Decimal values of One Pund payable after the number of years in the Margent, at the rate of 6 per Cent.|<609>
| Years. | Present va- lue of 1 l. |
Years. | Present va- lue of 1 l. |
Years. | Present va- lue of 1 l. |
|---|---|---|---|---|---|
| 1 | 0,9434 | 19 | 0,3305 | 37 | 0,1158 |
| 2 | 0,8900 | 20 | 0,3118 | 38 | 0,1092 |
| 3 | 0,8396 | 21 | 0,2941 | 39 | 0,1031 |
| 4 | 0,7921 | 22 | 0,2775 | 40 | 0,0972 |
| 5 | 0,7473 | 23 | 0,2618 | 45 | 0,0726 |
| 6 | 0,7050 | 24 | 0,2470 | 50 | 0,0543 |
| 7 | 0,6650 | 25 | 0,2330 | 55 | 0,0543 |
| 8 | 0,6274 | 26 | 0,2198 | 60 | 0,0303 |
| 9 | 0,5919 | 27 | 0,2074 | 65 | 0,0227 |
| 10 | 0,5584 | 28 | 0,1956 | 70 | 0,0169 |
| 11 | 0,5268 | 29 | 0,1845 | 75 | 0,0126 |
| 12 | 0,4970 | 30 | 0,1741 | 80 | 0,0094 |
| 13 | 0,4688 | 31 | 0,1747 | 85 | 0,0071 |
| 14 | 0,4423 | 32 | 0,1550 | 90 | 0,0053 |
| 15 | 0,4173 | 33 | 0,1462 | 95 | 0,0039 |
| 16 | 0,3936 | 34 | 0,1379 | 100 | 0,0029 |
| 17 | 0,3714 | 35 | 0,1301 | ||
| 18 | 0,3503 | 36 | 0,1227 |
It were needless to advertise, that the great trouble of working so many Proportions will be very much alleviated by using Logarithms; and that instead of using N n v-Y y υ for the Second Term of the Proportion in finding the value of Three Lives, it may suffice to use only Y y υ, and then deducting the Fourth Term so found out of the Third, the Remainder shall be the present value sought; or all these Fourth Terms being added together, and deducted out of the value of the certain Annuity for so many Yeares, will leave the value of hte contingent Annutity upon the Chance of Mortality of all those three Lives. For Example; Let there be Three Lives of 10, 30 and 40 years of Age proposed, and the Proportions will be thus:
| As 661 in 531 in 445 or 156190995, or N n v | ||
| to 8 in 8 in 9, or 576, or Y y v | for the first year, | so 0,9434 to 0,00000348 |
| to 15 in 16 in 18, or 4320, | for the second year, | so 0,8900 to 0,00002462 |
| to 21 in 24 in 28, or 13112 | for the third year, | so 0,8396 to 0,00008128 |
| to 27 in 32 in 38, | for the fourth year, | so 0.7921 to 0,00016650 |
| to 33 in 41 in 48, | for the fifth year, | so 0,7473 to 0,00031071 |
| to 39 in 50 in 58, | for the sixth year, | so 0.7050 to 0,00051051 |
|<610>
And so forth to the 60th year, when we suppose the elder Life of Forty certainly to be expired; from whence thill Seventy we must compute for the First and Second only, and from thence to Ninety for the single youngest Live. The the Sum Total of all these Fourth Proportionals being taken out of the value of a certian Annuity for 90 Years, bei 16,58 years Purchase, shall leave the just value to be paid for an Annutiy during the whole term of the Lives of three Persons of the Ages proposed. And more, that it will obt be necessary to compute for every year singly, but that in most cases every 4th or 5th year may suffice, interpoling for the intermediate years secundum artem.
It may be objected that the different Salubrity of places does hinder this Proposal from being universal; nor can it be denied. But by the number that die, being 1174 per Annum in 34000, it does appear that about a 30th part die yearly, as Sir William Petty has computed for London; and the number that die in Infancy, is a good Argument that the Air is but indifferently salubrious. So that by what I can learn, there cannot perhaps be one better place proposed for a Standard. At least ’tis desired that in imitation hereof the Curious in other Cities would attempt something of the same nature, that which nothing perhaps can be more useful.
SIR,
What I gave you in my former Discourse on these Bills, was chiefly designed for the Computation of the Values of Annuities on Lives, wherein I believe I have performed what the short Period of my Observations would permit, in relation to exactness, but at the same time do earnestly desire, that their Learned Author Dr. Newman* of Breslaw would please to continue them after the same manner for yet some years further, that so the casual Irregularities and apparent Discordance in the Table, p.599.* may by a certain number of Chances be rectified and ascertained.
Were this Calculus founded on the Experience of a very great number of Years, it would be very well worth the while to think of. Methods for facilitating the Computation of the Value of two, three, or more Lives; which as proposed in my former, seems (as I am inform’d) a Work of too much Difficulty for the ordinary Arithmetician to undertake. I have sought, if it were possible, to find a Theorem that might be more concise than the Rules there laid down, but in vain; for all that can be done to expedite it, is by Tables of Logarithms ready computed, to exhibit the Rationes of N to Y in each single Life, for every third, fourth or fifth Year of Age, as occasion shall require; and these Logarithms being added to the Logarithms of the present Value of Money payable after so many Years, will give a Series of Numbers, the Sum of which will show the Value of the Annuity sought. However for each Number of this Series two Logarithms for a single Life, three for two Lives, and four for three Lives, must necessarily be added together. If you think the matter, under the uncertainties I have mentioned, to deserve it, I shall shortly give you such a Table of Logarithms as I speak of, and an Example or two of the use thereof: But by Vulgar Arithmetick the labour of these Numbers were immense; and nothing will more recommend the useful Invention of Logarithms to all Lovers of Numbers, than the advantage of Dispatch in this and such like Computations.
Besides the uses mentioned in my former, it may perhaps not be an unacceptable thing to infer from the same Tables, how unjustly we repine at the shortness of our Lives, and think our selves wronged if we attain not Old Age; whereas it appears hereby, that the one half of those that are born are dead in Seventeen years time, 1238 being in that time reduced to 616.* So that instead of murmuring at what we call an untimely Death, we ought with Patience and unconcern to submit to that Dissolution which is the necessary Condition of our perishable Materials, and of our nice and frail Structure and Composition: And to account it as a Blessing that we have survived, perhaps by many Years, that Period of Life, whereat the one half of the whole Race of Mankind does not arrive.
A second Observation I make upon the said Table, is that the Growth and Encrease of Mankind is not so much stinted by any thing in the Nature of the Species, as it is from the cautious difficulty most People make to adventure on the state of Marriage, from the prospect of the Trouble and Charge of providing for a Family. Nor are the poorer sort of People herein to be blamed, since their difficulty of subsisting is occasioned by the unequal Distribution of Possessions, all being necessarily fed from the Earth, of which yet so few are Masters. So that besides themselves and Families, they are yet to work for those who own the Ground that feeds them: And of|<655> such does by very much the greater part of Mankind consist; otherwise it is plain, that there might well be four times as many Births as we now find. For by computation from the Table, I find that there are nearly 15000 Persons above 16 and under 45, of which at least 7000 are Women capable to bear Children. Of these notwithstanding there are but 1238 born yearly, which is but little more than a sixth part. So that about one in six of these Women do breed yearly; whereas were they all married, it would not appear strange or unlikely, that four of six should bring a Child every year. The Political Consequences hereof I shall not insist on, only the Strength and Glory of a King being in the multitude of his Subjects, I shall only hint, that above all things, Celibacy ought to be discouraged as, by extraordinary Taxing and Military Service: And those who have numerous Families of Children to be countenanced and encouraged by such Laws as the Jus trium Liberorum among the Romans. But especially, by an effectual Care to provide for the Subsistence of the Poor, by finding them Employments, whereby they may earn their Bread, without being chargeable to the Publick.|<656>
© Matthias Böhne, 16 January 2002